酒时柒
0%

图的基本概念

发表于 更新于

一、图的基本概念

  • 连通图/非连通图：图中任意一个节点都可以通过一条路径到达所有的其他节点即为连通图，否则为非连通图。
  • 带权图：图的边可以带权，用于描述从一个节点到另一个节点的开销。
  • 致密图/稀疏图：边与节点的比率决定一个图是稀疏的还是致密的。在设计算法时需要考虑图是稀疏图还是致密图。
  • 有向图/无向图：边是有方向的图即有向图。实际使用时，有时为了数据结构的统一，也会将无向图当作有向图处理（即每条边都是双向的）。

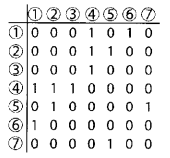
  • 邻接矩阵：邻接矩阵用一个二维矩阵表示图的连接关系。其空间开销是O(N^2)，对于稀疏图来说，大部分元素都会浪费，因此不是很经济。

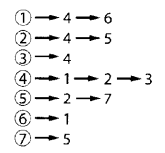
  • 邻接表：邻接表以链表的形式储存每一个节点连接的节点（边）。其空间开销是O(N+E)，因为游戏中使用的图大多数都为稀疏图，所以一般使用邻接表表示图。

  • 度/出度/入度：在无向图中，顶点 v 的度（Degree）是指依附于顶点 v 的边数，通常记为 TD(v)。在有向图中，顶点的度等于顶点的入度(In Degree)与顶点的出度之和。顶点v的入度是指以该顶点v为弧头的弧的数目，记为ID(v)；顶点 v 的出度（Out Degree）是指以该顶点 v 为弧尾的弧的数目，记为 OD(v)。所以，顶点 v 的度 TD(v)= ID(v) + OD(v)。

二、游戏中图的作用

导航图

  • 导航图包含了在一个游戏环境中智能体可以访问的所有位置和这些位置之间地所有连接。其中，节点通常表示关键区域的位置或者环境中的对象，边则代表了点与点之间的连接，边的开销可以根据具体的游戏定义，最简单的可以用两个节点之间的距离表示。
  • 智能体并非限制在只能沿着导航图的边移动，而是可以移动到环境内任何无障碍的位置，导航图的作用事规划路径，具体可以参考导航算法。

依赖图

  • 资源管理类游戏中，依赖图用来描述玩家可以利用的不同建筑物、材料、单元以及技术之间的依赖关系，可以清晰地显示每种类型的资源所需要的先决条件。

状态图

  • 状态图用于表示状态之间的切换关系，一个图就能表示一个问题的状态空间，其中节点表示可能的一种状态，边则表示两个状态之间的切换关系，比如Unity中的动画状态机。

三、图的邻接表实现

由于游戏中普遍使用的是稀疏图，因此之后的搜索算法都使用图的邻接表算法实现。

邻接表由两部分构成：顶点节点和邻接表节点。顶点节点顺序储存，邻接表节点链式储存，其链接表示两个节点之间的边。具体实现如下。

顶点数据类 Node<T>

为了通用和便于扩展，首先需要定义顶点数据类型，用于储存顶点的数据。

1
2
3
4
5
6
7
8
9
public class Node<T>
{
    public Node(T data)
    {
        Data = data;
    }

    public T Data { get; }
}

顶点节点类 VexNode<T>

顶点节点包含两个域，一个储存顶点数据，另一个为邻接表第一个节点的引用。

1
2
3
4
5
6
7
8
9
10
11
public class VexNode<T>
{
    public VexNode(Node<T> data, AdjNode<T> adjNode = null)
    {
        Data = data;
        FirstAdjNode = adjNode;
    }

    public Node<T> Data { get; }
    public AdjNode<T> FirstAdjNode { get; set; }
}

邻接表节点类 AdjNode<T>

邻接节点同样会储存顶点数据（为了方便查找对应的顶点节点）；边的数据也会存在邻接表节点中；以及，会包含一个指向下一个节点的引用。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public class AdjNode<T>
{
    public AdjNode(Node<T> data, float cost = 0, AdjNode<T> next = null)
    {
        Data = data;
        Next = next;
        Cost = cost;
    }

    public Node<T> Data { get;}
    
    public float Cost { get; set; }
    public AdjNode<T> Next { get; set; }
}

图类 Graph<T>

  • 图需要储存所有的顶点节点，一般会采用List，这里为了方便查询，使用一个字典储存顶点节点，用顶点数据作为Key，这样，就不用经常性地遍历List。

  • 由于顶点节点和邻接节点只有图知道，不对外暴露，所以外部代码只知道顶点数据类，图对外提供的各个方法中都以顶点数据类为参数。

  • 图需要对外提供各种基本的图操作方法，如判断节点、增删节点、判断边、增删边、修改边的权值等。
  • 为了兼容有向图和无向图，在添加（删除）边的时候，无向图会自动添加（删除）两遍，正向一遍，反向一遍。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
public class Graph<T> : IEnumerable<VexNode<T>>, IGraph<T>
{
    public Graph(Node<T>[] data)
    {
        NodeDic = new Dictionary<Node<T>, VexNode<T>>();
        foreach (var t in data)
        {
            NodeDic[t] = new VexNode<T>(t);
        }
    }

    public Graph()
    {
        NodeDic = new Dictionary<Node<T>, VexNode<T>>();
    }

    // 是否为有向图
    public bool IsDigraph { get; set; }

    // 顶点数目
    public int NodeNum => NodeDic.Count;

    // 边的数目
    public int EdgeNum
    {
        get
        {
            var count = 0;
            foreach (var node in NodeDic.Values)
            {
                var p = node.FirstAdjNode;
                while (p != null)
                {
                    ++count;
                    p = p.Next;
                }
            }

            return IsDigraph ? count : count / 2;
        }
    }

    public VexNode<T> this[Node<T> node]
    {
        get => NodeDic[node];
        set => NodeDic[node] = value;
    }


    private Dictionary<Node<T>, VexNode<T>> NodeDic;


    // 判断节点是否属于图
    public bool IsNode(Node<T> node)
    {
        return NodeDic.TryGetValue(node, out var _);
    }

    // 判断两点之间是否有边
    public bool HasEdge(Node<T> from, Node<T> to)
    {
        if (!IsNode(from) || !IsNode(to))
        {
            Debug.Log("节点不属于图！");
            return false;
        }

        var p = NodeDic[from].FirstAdjNode;
        while (p != null)
        {
            if (p.Data == to)
            {
                return true;
            }

            p = p.Next;
        }

        return false;
    }

	// 添加节点
    public void AddNode(Node<T> node)
    {
        if (IsNode(node))
        {
            Debug.LogError("已经存在节点！");
            return;
        }

        NodeDic[node] = new VexNode<T>(node);
    }

    // 在两节点之间添加边
    public void AddEdge(Node<T> from, Node<T> to, int cost = 1)
    {
        if (!IsNode(from) || !IsNode(to))
        {
            Debug.LogError("节点不属于图！");
            return;
        }

        if (HasEdge(from, to))
        {
            Debug.LogError("边已经存在！");
            return;
        }

        var p = new AdjNode<T>(to, cost);
        var firstNode = NodeDic[from].FirstAdjNode;
        if (firstNode == null)
        {
            NodeDic[from].FirstAdjNode = p;
        }
        else
        {
            p.Next = firstNode;
            NodeDic[from].FirstAdjNode = p;
        }

        if (IsDigraph) return;
        p = new AdjNode<T>(from, cost);
        firstNode = NodeDic[to].FirstAdjNode;
        if (firstNode == null)
        {
            NodeDic[to].FirstAdjNode = p;
        }
        else
        {
            p.Next = firstNode;
            NodeDic[to].FirstAdjNode = p;
        }
    }

    // 删除边
    public void RemoveEdge(Node<T> from, Node<T> to)
    {
        if (!IsNode(from) || !IsNode(to))
        {
            Debug.LogError("节点不属于图！");
            return;
        }

        if (!HasEdge(from, to))
        {
            Debug.LogError("边不存在！");
            return;
        }

        var p = NodeDic[from].FirstAdjNode;
        AdjNode<T> pre = null;
        while (p != null)
        {
            if (p.Data == to) break;
            pre = p;
            p = p.Next;
        }

        pre.Next = p.Next;

        if (IsDigraph) return;

        p = NodeDic[to].FirstAdjNode;
        pre = null;
        while (p != null)
        {
            if (p.Data == from) break;
            pre = p;
            p = p.Next;
        }

        pre.Next = p.Next;
    }

    // 改变边的值
    public void ChangeEdgeCost(Node<T> from, Node<T> to, float cost)
    {
        if (!IsNode(from) || !IsNode(to))
        {
            Debug.LogError("节点不属于图！");
            return;
        }

        if (!HasEdge(from, to))
        {
            Debug.LogError("边不存在！");
            return;
        }

        var p = NodeDic[from].FirstAdjNode;
        while (p != null)
        {
            if (p.Data == to) break;
            p = p.Next;
        }

        p.Cost = cost;

        if (IsDigraph) return;
        p = NodeDic[to].FirstAdjNode;
        while (p != null)
        {
            if (p.Data == from) break;
            p = p.Next;
        }

        p.Cost = cost;
    }

    public IEnumerator<VexNode<T>> GetEnumerator()
    {
        return NodeDic.Values.GetEnumerator();
    }

    IEnumerator IEnumerable.GetEnumerator()
    {
        return GetEnumerator();
    }
}

参考资料：

Demo地址：https://github.com/Luciano-0/Graph.git