一、最短路径问题
最短路径问题是一个基于开销的图搜索问题,指求解从图中的某一节点出发到达另一个节点经过所有边的开销和最小的路径。解决该问题的算法有:
- Dijkstra算法
- A*算法
- SPFA算法
- Floyd算法
二、Dijkstra
概述
Dijkstra用于解决图的单源最短路径问题,其前提为路径开销都为正值,使用贪心的思想进行边放松,其最终的结果是生成一棵最短路径树。
- 边放松指的是在查找最短路径过程中,如果碰到一条边,通过该边到达某一结点的路径比之前记录的到达该点的路径短,那么这个更短的路径将会取代之前的路径。可以把路径理解成从起点到某一点连接了一条橡皮筋,从下图的A->B操作,橡皮筋就得到了放松。
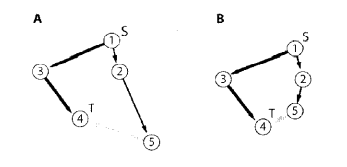
- 最短路径树(Short Path Tree,SPT)是图的一颗子树,其中根节点到某一子节点的路径就是这两节点在图中的最短路径。
思路
- 首先,我们需要一个数据结构用于储存各个节点搜索过程中产生的数据:其中包含是否已经找到最短路径的标志、从源节点到该节点当前路径的开销以及当前路径数组。
1 | private class Distance |
一开始需要将字典初始化,将除了源节点O之外的所有节点开销设为无穷大,源节点则为0。
接着进入循环,每次取未找到最短路径(found = false)且value最小的节点P,将found置为true,并遍历P的邻接节点,若遍历到的节点Q未找到最短路径,则检查通过P到达Q是否比Q原来的value小,若小则说明通过P到达Q为更优的路径,于是更新Q的value和path(这一步就是对O到Q的路径做了松弛),以此类推。
以上就是Dijkstra算法的关键部分,至于为什么每次要取value最小的节点P并且可以将P的found置为true,因为所有边的开销都为正值,而目前除了已找到最短路径的节点外,距离源节点O最近的是P,那么就不可能通过其他未知的路径,进一步缩短从源节点到达P的开销。这一步就是Dijkstra算法贪心思想的体现。
若没有输入目标节点,则算法可以找到从源节点到任一节点的最短路径,形成最短路径树;若输入了目标节点,则循环可以在目标节点的最短路径找到后返回。
栗子
- 以下图为例,假设源节点为0。
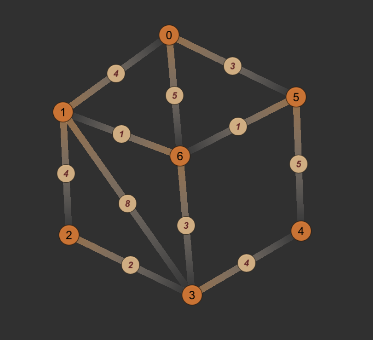
- 首先将字典初始化为:
| dis | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| value | 0 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| found | false | false | false | false | false | false | false |
| path | null | null | null | null | null | null | null |
- 第一次循环:取0节点,0->0的最短路径找到,更新0节点的found和path,然后遍历可从0节点到达的节点:5、6,更新他们的value和path。
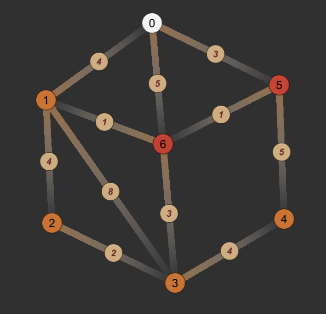
| dis | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| value | 0 | ∞ | ∞ | ∞ | ∞ | 3 | 5 |
| found | true | false | false | false | false | false | false |
| path | 0->0 | null | null | null | null | 0->5 | 0->6 |
- 第二次循环:取未找到最短路径节点中value最小的节点:5,0->5最短路径已找到,因为不可能通过其他节点,进一步缩短0->5的距离了,因此更新5节点的found和path,并遍历从5节点能到达的节点:6、4,发现0->5->6的路径优于0->6的路径,因此更新4和6节点的value和path。
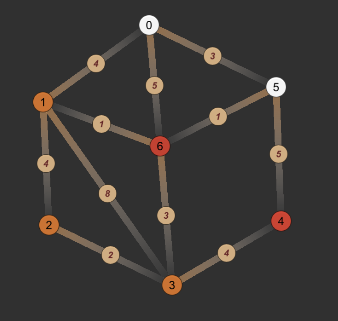
| dis | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| value | 0 | ∞ | ∞ | ∞ | 8 | 3 | 4 |
| found | true | false | false | false | false | true | false |
| path | 0->0 | null | null | null | 0->5->4 | 0->5 | 0->5->6 |
- 以此类推…
| dis | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| value | 0 | 5 | 9 | 7 | 8 | 3 | 4 |
| found | true | true | true | true | true | true | true |
| path | 0 | 0->5->6->1 | 0->5->6->1->2 | 0->5->6->3 | 0->5->4 | 0->5 | 0->5->6 |
实现
1 | public static class Dijkstra<T> |
优化
未经过优化的Dijkstra算法时间复杂度为O(n^2),而每次选最小节点的步骤可以使用堆进行优化,可以考虑使用二叉堆、二项堆或者斐波那契堆,优化后的时间复杂度计算可以参考:Dijkstra算法时间复杂度分析
三、A*
概述
Dijkstra算法在搜索过程中还是需要检查太多的边,在找到目标节点之前,算法会在各个方向上进行尝试。而A算法就是在Dijkstra算法的基础上引入了*启发函数的概念,大大地提高了搜索的效率。
思路
启发函数指的是对当前节点到目标节点开销的估计值,如果算法使用的启发函数是从任何节点到目标节点的实际开销的下限(低估开销得到),那么A*算法可以保证给出最优路径。如对于导航图最常用的启发函数就是节点之间的直线距离。
A*算法的工作方式和Dijkstra几乎一致,唯一的区别就是每个节点开销F的计算变成了:
G为到达一个节点的累计开销,H是一个启发函数。
实现
1 | public static class AStar<T> |
优化
结合Floyd算法
Floyd算法是预计算每一条可能的路径存在查找表中,这是实时寻路最快的一种算法(比A*快一个数量级),但其对空间的需求非常大。不过我们有办法通过压缩减少其对空间的需求,达到可接受的水平。
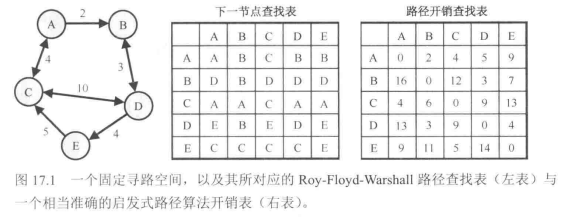
无损压缩:只存储关键的”换乘点“信息
在实际应用的寻路地图中,最佳路径的数量是有限的,而且多数重叠,因此我们可以找到最佳路径会经过的有限的”换乘点“,每个节点保存通往该节点所有换乘点的路径以及换乘点之间的最佳路径。
有损压缩:欧几里得嵌入算法
我们可以只储存查找表中的一部分行和列,这些数据可以成为枢纽节点来优化A*算法的启发函数,使得启发函数对距离的估算更加准确。
使用最恰当的搜索空间表征
- 常见的三种空间表征有:网格图、路点图、导航网格
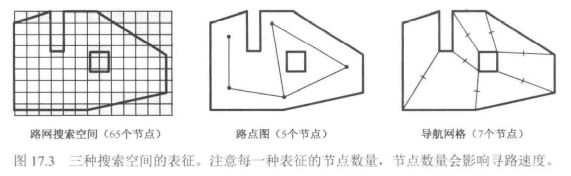
- 在大世界的地图中,以上三种空间表征可能性能开销都非常大,这时候就需要进行分层寻路。将较高的层级抽象为”区域到区域“的寻路方式,而较低的层级则抽象为”节点到节点“的寻路方式。
高估启发函数
低估启发函数可以保证找到最优路径,但有时可以适当高估启发函数,得到一条不那么优的路径,但是可以大幅度提高寻路性能。可以使用加权的启发函数:
其中w(x)可以位置变化而变化,如:当距离目标较远时,w(x)取较大值,牺牲一定的精确度,快速接近目标;当距离目标较小时,w(x)取较小值,精确地到达目标位置。
更好的启发函数
以网格图为例,可以选用三种启发函数:欧几里得距离(直线距离)、对角线距离和曼哈顿距离,曼哈顿距离不考虑对角线行走,总是高估距离,欧几里得距离总是低估距离,而对角线距离是最合适的启发函数:
开表的选择
通常情况下会选用堆来维护开表,但在节点数量较少时,采用简单的数组,插入开销小,查找需要遍历,但整体上对缓存友好,维护数据结构的开销几乎为0,因此寻路速度反而更快。
寻路期间请勿回溯
在网格图中存在许多短循环,而我们在寻路过程中不需要考虑那些与父节点临近的点,排除这些点可以避免许多多余的查找。这也是跳点寻路算法的思想:Jump Point Search(JPS)算法总结与实现
参考资料:
- 《人工智能编程案例精粹》第5章:图的秘密生命
- 《游戏人工智能》17:寻路架构的优化
- 最短路径问题—-Dijkstra算法详解
- Dijkstra算法时间复杂度分析