一、概述
游戏开发中随机是一个常用的工具,游戏程序员需要常常和rand()函数打交道,但是很多效果其实是无法通过简单的rand()函数实现的,需要更高级的随机技术。以下简单整理了《游戏人工智能》《代码本色》中介绍的几种高级随机技术,主要有:
- 高斯随机
- 随机值筛选
- 自定义分布的随机数
- 柏林噪声
二、高斯随机
问题
日常生活中许多现象在统计学上都满足高斯分布(即正态分布),其原因可以用中央极限定理来解释。在游戏中为了达到更真实更贴近自然的模拟,也要采用高斯随机,而不是简单的均匀随机。
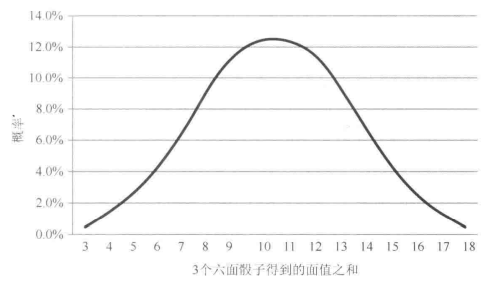
实现
生成高斯随机值的方法非常简单,只需要对三个均匀随机值求和,即可得到一组满足高斯分布的随机数。更准确地说,按照中央极限定理,对多个[-1, 1]范围内的均匀随机数求和,其结果会逼近均值为0、标准差为$\sqrt{K/3}$ 的高斯分布,其中K为参与求和的随机数数量。如果K值为3,则标准差等于1,那么我们就得到一个标准正态分布。
应用
高斯随机可以在游戏中得到广泛的应用,如:
- 模拟弹道
- NPC的平均或最大速度
- NPC的反应时间
- 暴击概率
- 体型大小、宽度、高度、质量等
为了达到更贴近真实的模拟,还可以进行叠加,如让每个NPC的基础射速呈高斯分布,而每一次射击还会在基础射速上按照高斯分布随机变化,这样就能达到非常自然的群体运动表现。
三、自定义分布的随机数
问题
现实中还存在许多例子不能用均匀分布或是高斯分布模拟,需要满足各种不同类型的分布,如指数分布、泊松分布、瑞利分布等。举个简单的例子:我们需要从[0, 1]中选出一个数,且数字越大,被选到的概率也越大,若选中概率为y,选中的值为x,可以简单地定义其映射关系为$y=x$。
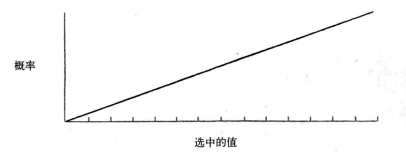
实现
自定义分布的随机数的生成有几种不同的方法,可以参考信号处理——生成给定分布随机数,这里介绍一种常见的方法:舍选法。
每次生成两个随机数,第一个是普通随机数,第二个作为“资格随机数”,用来决定第一个随机数的取舍。对于以上举的例子,具体计算步骤如下:
- 生成一个随机数R1 = 0.3
- 计算R1被选中的资格概率为0.3
- 生成另一个随机数R2
- 若R2 < R1,则R1就是我们要的随机数
- 否则,回到第一步重新开始
四、随机值筛选
问题
在游戏中,随机值过于随机也会存在问题,人们会认为少量的随机值不是随机生成的,比如游戏战斗中,敌方连续多次的暴击是完全有可能发生的,但对于玩家来说这样的体验就会很糟糕,甚至会开始怀疑游戏的机制或是作弊问题,因此作为开发者需要避免这样的情况产生,即让随机数序列看上去更随机。
应对策略
我们需要牺牲一点点随机完整性,换取一个看上去更加随机的序列。具体策略为:当生成一个随机数序列时,如果生成的下一个数会破坏随机性的表现,那就舍弃这个数然后再生成一个。具体策略可以参考《游戏人工智能:高级随机技术》,书中对于不同的情形有具体的应对策略。
值得注意的是,使用的筛选规则会影响到随机值的数学完整性,开源程序ENT提供了许多不同的度量标准来评估随机性。
五、柏林噪声
问题
游戏中会存在另一类随机需求:需要随机数之间存在连续性,即连续生成的随机数之间是有联系的,这种特性意味着我们不会在得到一个随机数之后得到一个差异很大的随机数。柏林噪声在图形学中有着广泛的应用,如用于生成大理石纹理、烟雾云彩、火焰等。

在游戏AI方面,柏林噪声可以控制角色在一段时间内的移动或属性变化,如:
- 角色移动(方向、速度、加速度)
- 精准度(连续的成功或失败,模拟运气势头)
- 注意力(警惕程度、反应时间)
- 角色情绪(冷静、愤怒、高兴、悲伤…)
一维柏林噪声的生成
- 首先确定频程,每阶频程在特定层次上影响信号细节,引入更高的频程可以增加更细粒度的信息,每阶频程独立计算,累加后得到最终的信号。
- 第一阶频程首先在[0, 1]范围内随机生成信号的起始和结束值,然后对这两个值做插值计算,得到中间值,理想的插值函数为$6t^5-15t^4+10t^3$,该函数在0和1处一阶导和二阶导都为0,即在过渡处会非常平滑。
- 对于N阶频程,选取$2^{n-1}+1$个均匀随机数并等距离放置,然后再对其进行插值。
- 对于每一阶的信号,还需要乘以一个放大倍数$p^i$,其中p为顽固指数,i为频程的阶数。对所有的信号叠加后就得到了最终的柏林噪声。下图中的例子就是一个阶数为4,顽固指数为0.5的柏林噪声生成过程。
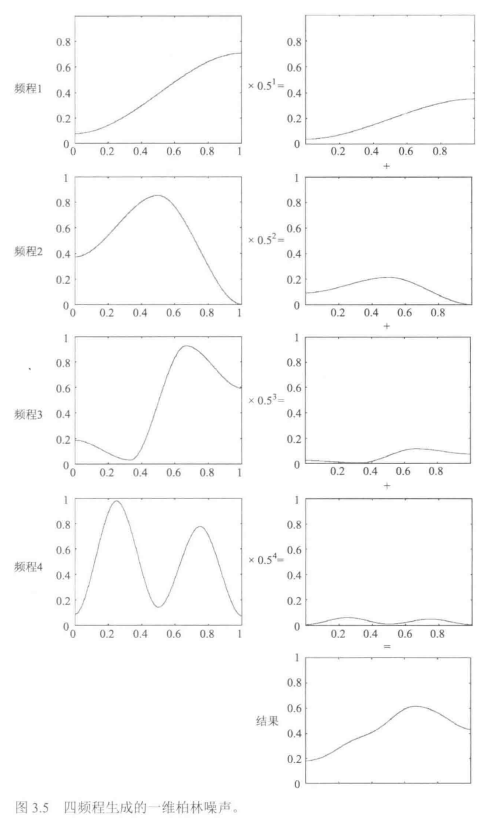
回顾以上的生成过程我们可以从中提取出几个重要的参数,通过改变他们的大小就能生成不同样式的柏林噪声。
- 频程的阶数:低阶频程在最终信号中造成更大的波动,而高阶的频程则导致更细粒度的噪声。
- 频程的范围:可以任意指定信号的频程范围来生成不同的最终信号。
- 每阶频程的放大倍数:可以通过改变每阶频程的放大倍数来决定该频程在最终信号中的权重。
- 插值函数的选择:$6t^5-15t^4+10t^3$为常用的插值函数,但也可以选择不同的插值函数来达到一些有趣的效果。
以上介绍一维柏林噪声的生成,但在图形学中用的更多的是二维柏林噪声,关于二维噪声的生成或是其他种类的噪声可以阅读【图形学】谈谈噪声
参考资料:
- 《游戏人工智能》第一部分3
- 《代码本色》第一章:引言
- 中心极限定理通俗介绍 - 知乎
- 信号处理——生成给定分布随机数
- 【图形学】谈谈噪声